Geometry Definition Of A Kite

Quadrilateral symmetric across a diagonal

Kite
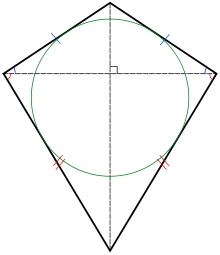A kite, showing its pairs of equal-length sides and its inscribed circle.
Blazon	Quadrilateral
Edges and vertices	4
Symmetry group	D 1 (*)

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are too known equally deltoids,^[1] but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connectedness with quadrilaterals.^{[two] [iii]} A kite may also exist called a dart,^[four] particularly if it is non convex.^{[5] [6]}

Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include every bit special cases the correct kites, with two contrary right angles; the rhombi, with 2 diagonal axes of symmetry; and the squares, which are too special cases of both right kites and rhombi.

The quadrilateral with the greatest ratio of perimeter to diameter is a kite, with 60°, 75°, and 150° angles. Kites of two shapes (i convex and one non-convex) course the prototiles of ane of the forms of the Penrose tiling. Kites also class the faces of several face-symmetric polyhedra and tessellations, and accept been studied in connection with outer billiards, a trouble in the advanced mathematics of dynamical systems.

Definition and classification [edit]

A kite is a quadrilateral with reflection symmetry across one of its diagonals. Equivalently, it is a quadrilateral whose four sides can exist grouped into two pairs of adjacent equal-length sides.^{[1] [7]} A kite can exist constructed from the centers and crossing points of any ii intersecting circles.^[viii] Kites as described here may be either convex or concave, although some sources restrict kite to hateful but convex kites. A quadrilateral is a kite if and merely if whatever one of the following weather condition is true:

• The four sides tin exist split into ii pairs of adjacent equal-length sides.^[seven]
• One diagonal crosses the midpoint of the other diagonal at a right angle, forming its perpendicular bisector.^[9] (In the concave case, the line through one of the diagonals bisects the other.)
• One diagonal is a line of symmetry. It divides the quadrilateral into 2 congruent triangles that are mirror images of each other.^[7]
• One diagonal bisects both of the angles at its two ends.^[7]

Kite quadrilaterals are named for the air current-diddled, flight kites, which often accept this shape^{[10] [eleven]} and which are in turn named for a hovering bird and the sound it makes.^{[12] [thirteen]} Co-ordinate to Olaus Henrici, the proper noun "kite" was given to these shapes by James Joseph Sylvester.^[fourteen]

Quadrilaterals tin exist classified hierarchically, meaning that some classes of quadrilaterals include other classes, or partitionally, meaning that each quadrilateral is in merely i class. Classified hierarchically, kites include the rhombi (quadrilaterals with 4 equal sides) and squares. All equilateral kites are rhombi, and all equiangular kites are squares. When classified partitionally, rhombi and squares would not be kites, because they belong to a dissimilar grade of quadrilaterals; similarly, the correct kites discussed below would not be kites. The residue of this commodity follows a hierarchical classification; rhombi, squares, and right kites are all considered kites. By avoiding the need to consider special cases, this classification can simplify some facts about kites.^[15]

Similar kites, a parallelogram too has 2 pairs of equal-length sides, but they are opposite to each other rather than adjacent. Any non-self-crossing quadrilateral that has an centrality of symmetry must be either a kite, with a diagonal axis of symmetry; or an isosceles trapezoid, with an axis of symmetry through the midpoints of two sides. These include as special cases the rhombus and the rectangle respectively, and the square, which is a special case of both.^[i] The self-crossing quadrilaterals include another class of symmetric quadrilaterals, the antiparallelograms.^[16]

Special cases [edit]

The right kites have ii reverse right angles.^{[15] [16]} The right kites are exactly the kites that are cyclic quadrilaterals, meaning that there is a circle that passes through all their vertices.^[17] The cyclic quadrilaterals may equivalently defined equally the quadrilaterals in which two contrary angles are supplementary (they add together to 180°); if one pair is supplementary the other is too.^[9] Therefore, the right kites are the kites with 2 reverse supplementary angles, for either of the two opposite pairs of angles. Because right kites delimit i circle and are inscribed in another circle, they are bicentric quadrilaterals (actually tricentric, as they as well have a third circle externally tangent to the extensions of their sides).^[16] If the sizes of an inscribed and a circumscribed circle are fixed, the right kite has the largest area of whatsoever quadrilateral trapped between them.^[xviii]

Among all quadrilaterals, the shape that has the greatest ratio of its perimeter to its diameter is an equidiagonal kite with angles 60°, 75°, 150°, 75°. Its iv vertices lie at the three corners and i of the side midpoints of the Reuleaux triangle.^{[nineteen] [20]} When an equidiagonal kite has side lengths less than or equal to its diagonals, like this ane or the square, it is one of the quadrilaterals with the greatest ratio of area to diameter.^[21]

A kite with three 108° angles and 1 36° bending forms the convex hull of the lute of Pythagoras, a fractal made of nested pentagrams.^[22] The iv sides of this kite lie on four of the sides of a regular pentagon, with a golden triangle glued onto the 5th side.^[sixteen]

There are only eight polygons that can tile the airplane such that reflecting whatsoever tile across any 1 of its edges produces another tile; this arrangement is called an edge tessellation. One of them is a tiling by a right kite, with 60°, ninety°, and 120° angles. It produces the deltoidal trihexagonal tiling (see § Tilings and polyhedra).^[23]

In non-Euclidean geometry, a kite tin can have iii right angles and one non-right angle, forming a special case of a Lambert quadrilateral. The fourth angle is acute in hyperbolic geometry and obtuse in spherical geometry.^[24]

Properties [edit]

Diagonals, angles, and area [edit]

Every kite is an orthodiagonal quadrilateral, significant that its two diagonals are at right angles to each other. Moreover, one of the two diagonals (the symmetry axis) is the perpendicular bisector of the other, and is also the angle bisector of the two angles information technology meets.^[ane] Because of its symmetry, the other 2 angles of the kite must be equal.^{[10] [eleven]} The diagonal symmetry axis of a convex kite divides information technology into two congruent triangles; the other diagonal divides it into 2 isosceles triangles.^[1]

As is truthful more more often than not for any orthodiagonal quadrilateral, the area ${\displaystyle A}$ of a kite may be calculated as half the production of the lengths of the diagonals ${\displaystyle p}$ and ${\displaystyle q}$ :^[10]

$${\displaystyle A={\frac {p\cdot q}{2}}.}$$

Alternatively, the surface area can be calculated by dividing the kite into 2 congruent triangles and applying the SAS formula for their area. If ${\displaystyle a}$ and ${\displaystyle b}$ are the lengths of two sides of the kite, and ${\displaystyle \theta }$ is the angle between, so the surface area is^[25]

$${\displaystyle \displaystyle A=ab\cdot \sin \theta .}$$

Inscribed circle [edit]

Two circles tangent to the sides and extended sides of a convex kite (top), non-convex kite (middle), and antiparallelogram (bottom). The four lines through the sides of each quadrilateral are bitangents of the circles.

Every convex kite is also a tangential quadrilateral, a quadrilateral that has an inscribed circumvolve. That is, at that place exists a circle that is tangent to all 4 sides. Additionally, if a convex kite is not a rhombus, at that place is a circle outside the kite that is tangent to the extensions of the four sides; therefore, every convex kite that is not a rhombus is an ex-tangential quadrilateral. The convex kites that are non rhombi are exactly the quadrilaterals that are both tangential and ex-tangential.^[16] For every concave kite there exist two circles tangent to two of the sides and the extensions of the other two: i is interior to the kite and touches the two sides contrary from the concave angle, while the other circumvolve is exterior to the kite and touches the kite on the two edges incident to the concave angle.^[26]

For a convex kite with diagonal lengths ${\displaystyle p}$ and ${\displaystyle q}$ and side lengths ${\displaystyle a}$ and ${\displaystyle b}$ , the radius ${\displaystyle r}$ of the inscribed circle is

$${\displaystyle r={\frac {pq}{ii(a+b)}},}$$

and the radius ${\displaystyle \rho }$ of the ex-tangential circle is^[16]

$${\displaystyle \rho ={\frac {pq}{2|a-b|}}.}$$

A tangential quadrilateral is also a kite if and only if whatever ane of the following conditions is truthful:^[27]

• The area is one half the product of the diagonals.
• The diagonals are perpendicular. (Thus the kites are exactly the quadrilaterals that are both tangential and orthodiagonal.)
• The two line segments connecting opposite points of tangency take equal length.
• The tangent lengths, distances from a point of tangency to an adjacent vertex of the quadrilateral, are equal at two opposite vertices of the quadrilateral. (At each vertex, at that place are 2 adjacent points of tangency, but they are the aforementioned distance equally each other from the vertex, so each vertex has a single tangent length.)
• The two bimedians, line segments connecting midpoints of opposite edges, take equal length.
• The products of opposite side lengths are equal.
• The center of the incircle lies on a line of symmetry that is also a diagonal.

If the diagonals in a tangential quadrilateral ${\displaystyle ABCD}$ intersect at ${\displaystyle P}$ , and the incircles of triangles ${\displaystyle ABP}$ , ${\displaystyle BCP}$ , ${\displaystyle CDP}$ , ${\displaystyle DAP}$ have radii ${\displaystyle r_{1}}$ , ${\displaystyle r_{ii}}$ , ${\displaystyle r_{3}}$ , and ${\displaystyle r_{4}}$ respectively, then the quadrilateral is a kite if and simply if^[27]

$${\displaystyle r_{one}+r_{3}=r_{ii}+r_{4}.}$$

If the excircles to the same four triangles reverse the vertex ${\displaystyle P}$ have radii ${\displaystyle R_{one}}$ , ${\displaystyle R_{two}}$ , ${\displaystyle R_{iii}}$ , and ${\displaystyle R_{4}}$ respectively, then the quadrilateral is a kite if and only if^[27]

$${\displaystyle R_{1}+R_{3}=R_{2}+R_{iv}.}$$

Duality [edit]

A kite and its dual isosceles trapezoid

Kites and isosceles trapezoids are dual to each other, pregnant that there is a correspondence between them that reverses the dimension of their parts, taking vertices to sides and sides to vertices. From whatever kite, the inscribed circle is tangent to its four sides at the four vertices of an isosceles trapezoid. For any isosceles trapezoid, tangent lines to the circumscribing circumvolve at its four vertices grade the four sides of a kite. This correspondence can also be seen as an example of polar reciprocation, a general method for corresponding points with lines and vice versa given a fixed circle. Although they practice not impact the circle, the iv vertices of the kite are reciprocal in this sense to the four sides of the isosceles trapezoid.^[28] The features of kites and isosceles trapezoids that correspond to each other under this duality are compared in the table below.^[7]

Isosceles trapezoid	Kite
Ii pairs of equal adjacent angles	Two pairs of equal adjacent sides
Two equal opposite sides	Two equal reverse angles
Two opposite sides with a shared perpendicular bisector	2 contrary angles with a shared angle bisector
An centrality of symmetry through two opposite sides	An axis of symmetry through two opposite angles
Circumscribed circle through all vertices	Inscribed circle tangent to all sides

Autopsy [edit]

The equidissection trouble concerns the subdivision of polygons into triangles that all have equal areas. In this context, the spectrum of a polygon is the gear up of numbers ${\displaystyle northward}$ such that the polygon has an equidissection into ${\displaystyle north}$ equal-surface area triangles. Because of its symmetry, the spectrum of a kite contains all even integers. Certain special kites likewise comprise some odd numbers in their spectra.^{[29] [30]}

Every triangle can be subdivided into three right kites meeting at the center of its inscribed circle. More than generally, a method based on circle packing can be used to subdivide any polygon with ${\displaystyle north}$ sides into ${\displaystyle O(north)}$ kites, meeting edge-to-edge.^[31]

Tilings and polyhedra [edit]

Recursive construction of the kite and dart Penrose tiling

Fractal rosette of Penrose kites

All kites tile the plane by repeated indicate reflection around the midpoints of their edges, as exercise more than generally all quadrilaterals.^[32] Kites and darts with angles 72°, 72°, 72°, 144° and 36°, 72°, 36°, 216°, respectively, form the prototiles of i version of the Penrose tiling, an aperiodic tiling of the plane discovered by mathematical physicist Roger Penrose.^[v] When a kite has angles that, at its apex and 1 side, sum to ${\displaystyle \pi (1-{\tfrac {i}{n}})}$ for some positive integer ${\displaystyle n}$ , then scaled copies of that kite tin be used to tile the aeroplane in a fractal rosette in which successively larger rings of ${\displaystyle north}$ kites surround a cardinal signal.^[33] These rosettes can be used to study the miracle of inelastic plummet, in which a arrangement of moving particles meeting in inelastic collisions all coalesce at a mutual point.^[34]

A kite with angles 60°, xc°, 120°, 90° tin also tile the plane by repeated reflection beyond its edges; the resulting tessellation, the deltoidal trihexagonal tiling, superposes a tessellation of the airplane past regular hexagons and isosceles triangles.^[sixteen] The deltoidal icositetrahedron, deltoidal hexecontahedron, and trapezohedron are polyhedra with congruent kite-shaped faces,^[35] which tin alternatively be thought of equally tilings of the sphere by congruent spherical kites.^[36] In that location are infinitely many face up-symmetric tilings of the hyperbolic plane by kites.^[37] These polyhedra (equivalently, spherical tilings), the square and deltoidal trihexagonal tilings of the Euclidean aeroplane, and some tilings of the hyperbolic airplane are shown in the table below, labeled by confront configuration (the numbers of neighbors of each of the 4 vertices of each tile). Some polyhedra and tilings appear twice, nether two different face configurations.

Polyhedra			Euclidean
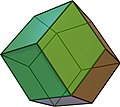V4.3.4.3	V4.3.4.4	V4.three.4.5	V4.three.four.6
Polyhedra	Euclidean	Hyperbolic tilings
V4.iv.four.3	V4.four.4.4	V4.iv.iv.five	V4.4.4.vi
Polyhedra	Hyperbolic tilings
V4.three.iv.5	V4.4.4.five	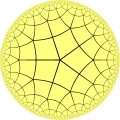V4.5.4.five	V4.vi.4.v
Euclidean	Hyperbolic tilings
V4.3.iv.6	V4.4.4.half dozen	V4.5.iv.6	V4.6.4.half-dozen

The trapezohedra are another family of polyhedra that have coinciding kite-shaped faces. In these polyhedra, the edges of one of the two side lengths of the kite run across at two "pole" vertices, while the edges of the other length grade an equatorial zigzag path around the polyhedron. They are the dual polyhedra of the uniform antiprisms.^[35] A commonly seen example is the pentagonal trapezohedron, used for ten-sided dice.^[sixteen]

Family of n-gonal trapezohedra

Name	Digonal trapezohedron (Tetrahedron)	Trigonal	Tetragonal	Pentagonal	Hexagonal	Heptagonal	Octagonal	...	Apeirogonal
Polyhedron								...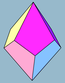
Tessellation								...
Face configuration	V2.3.3.3	V3.3.3.three	V4.three.3.iii	V5.three.3.3	V6.iii.3.3	V7.iii.3.3	V8.3.iii.3	...	V∞.3.3.3

Outer billiards [edit]

Mathematician Richard Schwartz has studied outer billiards on kites. Outer billiards is a dynamical system in which, from a point outside a given compact convex set in the plane, one draws a tangent line to the convex set, travels from the starting signal forth this line to some other point equally far from the point of tangency, and then repeats the same process. It had been open since the 1950s whether any arrangement defined in this way could produce paths that get arbitrarily far from their starting point, and in a 2007 paper Schwartz solved this trouble by finding unbounded billiards paths for the kite with angles 72°, 72°, 72°, 144°, the same equally the 1 used in the Penrose tiling.^[38] He later wrote a monograph analyzing outer billiards for kite shapes more by and large. For this problem, whatsoever affine transformation of a kite preserves the dynamical properties of outer billiards on it, and information technology is possible to transform any kite into a shape where three vertices are at the points ${\displaystyle (-one,0)}$ and ${\displaystyle (0,\pm 1)}$ , with the fourth at ${\displaystyle (\alpha ,0)}$ with ${\displaystyle \alpha }$ in the open unit interval ${\displaystyle (0,1)}$ . The behavior of outer billiards on any kite depends strongly on the parameter ${\displaystyle \alpha }$ and in particular whether it is rational. For the case of the Penrose kite, ${\displaystyle \alpha =1/\varphi ^{3}}$ , an irrational number, where ${\displaystyle \varphi =(1+{\sqrt {5}})/ii}$ is the golden ratio.^[39]

References [edit]

1. ^ ^{a b c d e} Halsted, George Bruce (1896), "Chapter Xiv. Symmetrical Quadrilaterals", Elementary Synthetic Geometry, J. Wiley & sons, pp. 49–53
2. ^ Goormaghtigh, R. (1947), "Orthopolar and isopolar lines in the cyclic quadrilateral", The American Mathematical Monthly, 54: 211–214, doi:10.1080/00029890.1947.11991815, JSTOR 2304700, MR 0019934
3. ^ Come across H. S. G. Coxeter's review of Grünbaum (1960) in MR0125489: "It is unfortunate that the writer uses, instead of 'kite', the name 'deltoid', which belongs more properly to a bend, the three-cusped hypocycloid."
4. ^ Charter, Kevin; Rogers, Thomas (1993), "The dynamics of quadrilateral folding", Experimental Mathematics, ii (3): 209–222, doi:x.1080/10586458.1993.10504278, MR 1273409
5. ^ ^{a b} Gardner, Martin (January 1977), "Extraordinary nonperiodic tiling that enriches the theory of tiles", Mathematical Games, Scientific American, vol. 236, no. 1, pp. 110–121, Bibcode:1977SciAm.236a.110G, doi:10.1038/scientificamerican0177-110, JSTOR 24953856
6. ^ Thurston, William P. (1998), "Shapes of polyhedra and triangulations of the sphere", in Rivin, Igor; Rourke, Colin; Series, Caroline (eds.), The Epstein birthday schrift, Geometry & Topology Monographs, vol. ane, Coventry: Geometry & Topology Publications, pp. 511–549, arXiv:math/9801088, doi:10.2140/gtm.1998.1.511, MR 1668340
7. ^ ^{a b c d e} De Villiers, Michael (2009), Some Adventures in Euclidean Geometry, p. sixteen, 55, ISBN978-0-557-10295-two
8. ^ Szecsei, Denise (2004), The Complete Idiot'south Guide to Geometry, Penguin, pp. 290–291, ISBN9781592571833
9. ^ ^{a b} Usiskin, Zalman; Griffin, Jennifer (2008), The Classification of Quadrilaterals: A Study of Definition, Data Historic period Publishing, pp. 49–52, 63–67
10. ^ ^{a b c} Beamer, James E. (May 1975), "The tale of a kite", The Arithmetics Teacher, 22 (5): 382–386, doi:x.5951/at.22.five.0382, JSTOR 41188788
11. ^ ^{a b} Alexander, Daniel C.; Koeberlein, Geralyn M. (2014), Elementary Geometry for Higher Students (6th ed.), Cengage Learning, pp. 180–181, ISBN9781285965901
12. ^ Suay, Juan Miguel; Teira, David (2014), "Kites: the rise and fall of a scientific object" (PDF), Nuncius, 29 (2): 439–463, doi:ten.1163/18253911-02902004
13. ^ Liberman, Anatoly (2009), Word Origins...And How We Know Them: Etymology for Everyone, Oxford University Press, p. 17, ISBN9780195387070
14. ^ Henrici, Olais (1879), Elementary Geometry: Congruent Figures, Longmans, Light-green, p. xiv
15. ^ ^{a b} De Villiers, Michael (Feb 1994), "The office and function of a hierarchical classification of quadrilaterals", For the Learning of Mathematics, xiv (1): 11–18, JSTOR 40248098
16. ^ ^{a b c d due east f one thousand h} Alsina, Claudi; Nelsen, Roger B. (2020), "Department iii.iv: Kites", A Cornucopia of Quadrilaterals, The Dolciani Mathematical Expositions, vol. 55, Providence, Rhode Island: MAA Press and American Mathematical Order, pp. 73–78, ISBN978-1-4704-5312-1, MR 4286138 ; encounter also antiparallelograms, p. 212
17. ^ Gant, P. (1944), "A notation on quadrilaterals", The Mathematical Gazette, 28 (278): 29–thirty, doi:10.2307/3607362, JSTOR 3607362
18. ^ Josefsson, Martin (2012), "Maximal area of a bicentric quadrilateral" (PDF), Forum Geometricorum, 12: 237–241, MR 2990945
19. ^ Brawl, D. Thou. (1973), "A generalisation of ${\displaystyle \pi }$ ", The Mathematical Gazette, 57 (402): 298–303, doi:10.2307/3616052, JSTOR 3616052
20. ^ Griffiths, David; Culpin, David (1975), "Pi-optimal polygons", The Mathematical Gazette, 59 (409): 165–175, doi:10.2307/3617699, JSTOR 3617699
21. ^ Audet, Charles; Hansen, Pierre; Svrtan, Dragutin (2021), "Using symbolic calculations to decide largest pocket-sized polygons", Periodical of Global Optimization, 81 (1): 261–268, doi:10.1007/s10898-020-00908-westward, MR 4299185
22. ^ Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 260, ISBN9780471667001
23. ^ Kirby, Matthew; Umble, Ronald (2011), "Edge tessellations and postage folding puzzles", Mathematics Magazine, 84 (4): 283–289, arXiv:0908.3257, doi:10.4169/math.mag.84.4.283, MR 2843659, S2CID 123579388
24. ^ Eves, Howard Whitley (1995), College Geometry, Jones & Bartlett Learning, p. 245, ISBN9780867204759
25. ^ "OC506" (PDF), Olympiad Corner Solutions, Crux Mathematicorum, 47 (5): 241, May 2021
26. ^ Wheeler, Roger F. (1958), "Quadrilaterals", The Mathematical Gazette, 42 (342): 275–276, doi:10.2307/3610439, JSTOR 3610439
27. ^ ^{a b c} Josefsson, Martin (2011), "When is a tangential quadrilateral a kite?" (PDF), Forum Geometricorum, 11: 165–174
28. ^ Robertson, Southward. A. (1977), "Classifying triangles and quadrilaterals", The Mathematical Gazette, 61 (415): 38–49, doi:10.2307/3617441, JSTOR 3617441
29. ^ Kasimatis, Elaine A.; Stein, Sherman 1000. (December 1990), "Equidissections of polygons", Discrete Mathematics, 85 (3): 281–294, doi:10.1016/0012-365X(90)90384-T, MR 1081836, Zbl 0736.05028
30. ^ Jepsen, Charles H.; Sedberry, Trevor; Hoyer, Rolf (2009), "Equidissections of kite-shaped quadrilaterals" (PDF), Involve, a Periodical of Mathematics, 2 (1): 89–93, doi:x.2140/involve.2009.2.89, MR 2501347
31. ^ Bern, Marshall; Eppstein, David (2000), "Quadrilateral meshing past circle packing", International Periodical of Computational Geometry and Applications, 10 (4): 347–360, arXiv:cs.CG/9908016, doi:10.1142/S0218195900000206, MR 1791192
32. ^ Schattschneider, Doris (1993), "The fascination of tiling", in Emmer, Michele (ed.), The Visual Heed: Art and Mathematics, Leonardo Book Series, Cambridge, Massachusetts: MIT Press, pp. 157–164, ISBN0-262-05048-X, MR 1255846
33. ^ Fathauer, Robert (2018), "Art and recreational math based on kite-tiling rosettes", in Torrence, Eve; Torrence, Bruce; Séquin, Carlo; Fenyvesi, Kristóf (eds.), Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture, Phoenix, Arizona: Tessellations Publishing, pp. 15–22, ISBN978-one-938664-27-iv
34. ^ Chazelle, Bernard; Karntikoon, Kritkorn; Zheng, Yufei (2022), "A geometric approach to inelastic plummet", Journal of Computational Geometry, thirteen (1): 197–203, doi:10.20382/jocg.v13i1a7, MR 4414332
35. ^ ^{a b} Grünbaum, B. (1960), "On polyhedra in ${\displaystyle Due east^{3}}$ having all faces congruent", Bulletin of the Research Council of Israel, 8F: 215–218 (1960), MR 0125489
36. ^ Sakano, Yudai; Akama, Yohji (2015), "Anisohedral spherical triangles and classification of spherical tilings by congruent kites, darts and rhombi", Hiroshima Mathematical Journal, 45 (three): 309–339, MR 3429167
37. ^ Dunham, Douglas; Lindgren, John; Witte, Dave (1981), "Creating repeating hyperbolic patterns", in Green, Doug; Lucido, Tony; Fuchs, Henry (eds.), Proceedings of the 8th Annual Briefing on Computer Graphics and Interactive Techniques, SIGGRAPH 1981, Dallas, Texas, U.s.a., Baronial iii–vii, 1981, Association for Computing Machinery, pp. 215–223, doi:ten.1145/800224.806808
38. ^ Schwartz, Richard Evan (2007), "Unbounded orbits for outer billiards, I", Journal of Modern Dynamics, i (3): 371–424, arXiv:math/0702073, doi:10.3934/jmd.2007.1.371, MR 2318496
39. ^ Schwartz, Richard Evan (2009), Outer Billiards on Kites, Annals of Mathematics Studies, vol. 171, Princeton, New Jersey: Princeton University Press, doi:10.1515/9781400831975, ISBN978-0-691-14249-4, MR 2562898

External links [edit]

Wikimedia Commons has media related to Deltoids.

• Weisstein, Eric W., "Kite", MathWorld
• area formulae with interactive animation at Mathopenref.com

Geometry Definition Of A Kite,

Source: https://en.wikipedia.org/wiki/Kite_(geometry)

Posted by: jacobsthujered.blogspot.com

Share this post